by Takis Angelides
In this article we will explore the capability of a popular form of tensor networks called matrix product states (MPS) [1] in compressing the amount of data we keep in memory during simulations of computational fluid dynamics (CFD).
High dimensional tensors are ubiquitous in the sciences having applications in quantum physics, general relativity, machine learning, fluid dynamics and many more. An MPS is a way to express a high dimensional tensor as a product of lower dimensional tensors. This gives us the ability to compress the amount of information we keep from the original tensor in a controlled manner such that only irrelevant information are discarded. The parameter that controls this is the so called bond dimension D which determines the size of the lower dimensional tensors.
The model we will use to exemplify the power of MPS is the Burger’s equation which has applications in turbulence modelling, shock wave formation, acoustics, traffic flow, heat conduction and diffusion processes. The Burger’s equation is given by
The u = u(t, x) here is the velocity field of the fluid, which is a function of time and of the one dimensional space axis. The first term on the left gives the rate of change of the velocity while the second term is a non-linear convective term giving the property that a wave moves faster where it develops higher velocities leading to the formation of shocks over time. The term on the right is a viscous term which causes resistance to flow and has the effect of smoothing out rapid changes or fluctuations in the velocity field.
Now our methodology is that first we will discretize x and the differential operators in Eq. (1). We express u(t, x) as an MPS and the differential operators as matrix product operators (MPO) which act on MPS [2]. Using periodic boundary conditions such that the lattice of points discretizing x is a circle, the goal is to evolve u(t, x) in time according to Eq. (1) given an initial condition
The bond dimension D which controls the compression we apply will be set such that the maximum error incurred from discarding some data is approximately of the order 10−15.
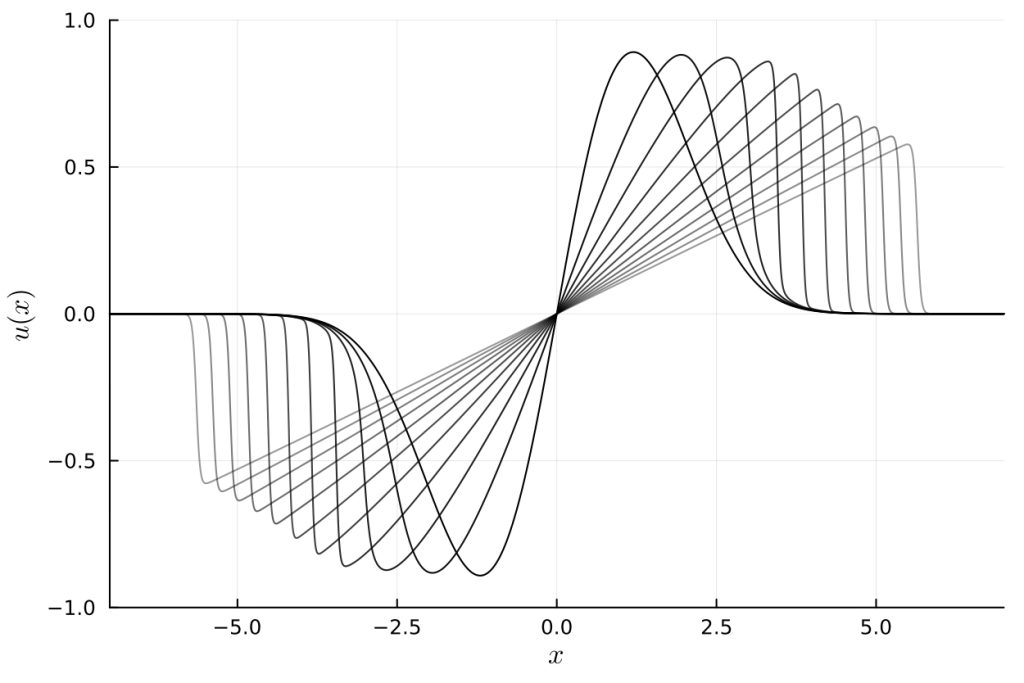
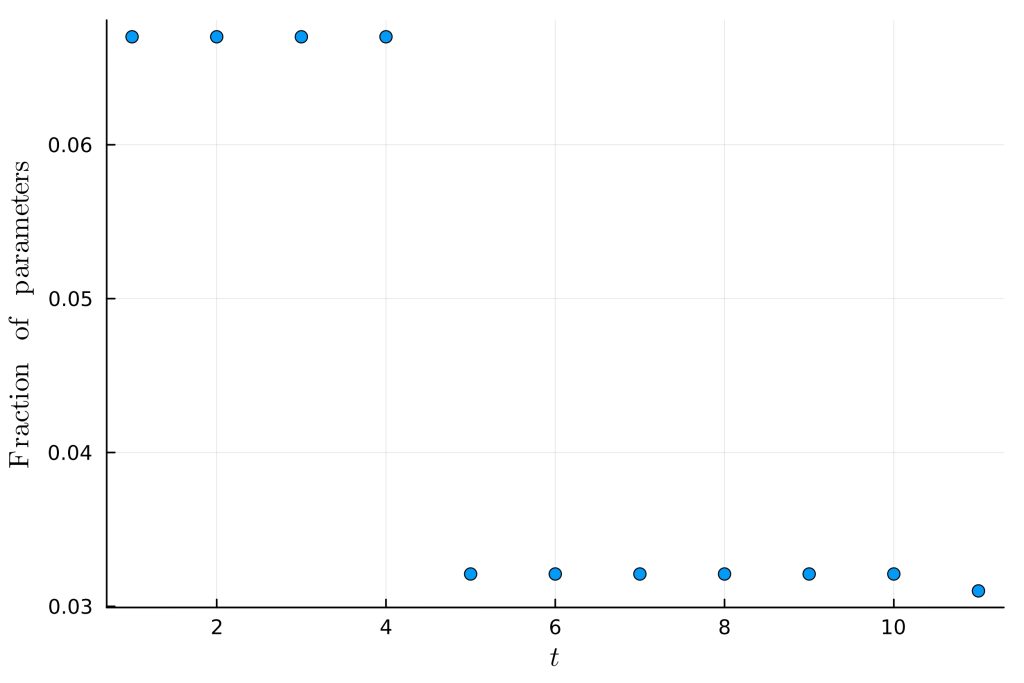
In Figure 1 we see the evolution of the velocity field where lighter colour indicates later times. The field moves as expected showing consistent behaviour with other general methods for CFD dynamics and demonstrates the formation of shocks at later times. Figure 2 shows the fraction of parameters kept in memory as compared to the case when no compression is applied. It suggests that only 3% of the data a direct numerical simulation would use was necessary to reproduce the well known dynamics of the Burger’s equation to high precision. Note we have 214 spatial lattice points hence the number of parameters to keep track of without compression is 214 real numbers at any given time.
In conclusion, we have demonstrated that tensor networks can achieve significant compression for CFD simulations. This implies they form a promising tool for the quest of probing turbulence, a notoriously difficult task for standard CFD methods due to the numerical demands of such an endeavor.
References
- Orus, R. A practical introduction to tensor networks: Matrix product states and projected entangled pair states. Annals of Physics 349, 117–158. issn: 0003-4916. https://www.sciencedirect.com/science/article/pii/S0003491614001596 (2014).
- Gourianov, N. et al. A quantum-inspired approach to exploit turbulence structures. Nature Computational Science 2, 30–37. https://doi.org/10.1038/s43588-021-00181-1 (2022).