by Peter Majcen
Quantum mechanics is often regarded as a hard topic to understand, and indeed, the subject can be quite intimidating, since it introduces concepts that are counter-intuitive to our day-to-day experience of nature. Popular science articles are often not easy to grasp, as there is a fine line between providing a simple answer and misrepresenting the concept. This often leads to confusion around terms like wave -particle duality, superposition, teleportation, quantum computing, and, of course, entanglement, just to name a few. In this article, I will try to give an intuitive picture of how entanglement makes it difficult to study quantum many-body systems and provide an idea of the techniques developed to overcome this issue. In quantum many-body physics, one studies the behavior and properties of a system that is a collection of many constituents, where each constituent is described by the laws of quantum mechanics.
To get an idea of such a “many-body” system and its entanglement, we will look at a system consisting of two quantum mechanical coins [1]. The first subsystem is called Allan (system A), and the second Barbie (system B). Classically, each of these coins must be either heads (H) or tails (T), but in quantum mechanics, the coin can be in a superposition of these two basis states. Thus, the states Iψ⟩A,B in the respective subsystems are of the form
Here, it is important to note that to characterize the state spaces SA and SB of Allan and Barbie, respectively, it is enough to specify the basis states I H ⟩ and I T ⟩.
Now, the question is how to combine these two systems, or in other words, what is the state space of the combined system – let’s call it SAB. The answer is to form the tensor product of the state spaces SA and SB. Mathematically, this combination is denoted by the tensor product
but this is just notation. To define SAB, it is again enough to specify its basis vectors, and the basis is exactly what you would expect, they are simply all the possible combinations of labels from the basis vectors of Allan and Barbie.
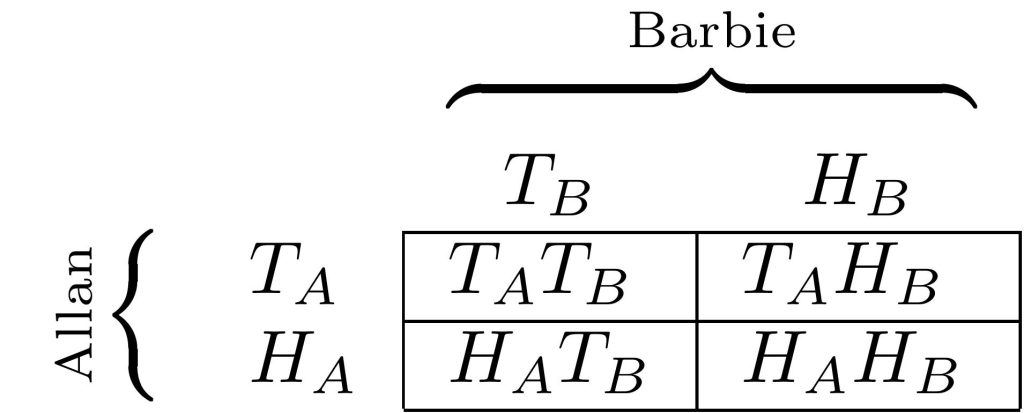
In the combined system, we have two different kinds of states, states that can be written as a product.
and states that cannot be written as such a product. An example of such a state is
Why this state cannot be written as a product state is actually easy to see. We just need to compare coefficients with our product state. Since there is no term I HH ⟩ in the singlet state, either αH or βH has to be zero. However, if either is zero, there would be no term proportional to I HT ⟩ or I TH ⟩. States that cannot be written in product form are the entangled states in our combined system. Although a state is either a product state or it is not, entanglement is not an all-or-nothing proposition; some entangled states can be more entangled than others. Our example state, I singlet ⟩, is a maximally entangled state. Maximally entangled states are actually of great interest in the field of quantum information theory because, although they provide a complete description of the state in the combined system, nothing is known about the individual subsystems of Allan and Barbie. In a product state, if I know the state of the combined system, I know everything there is to know about each respective subsystem. In other words, Allan is completely independent of Barbie and vice versa (there are no correlations between the two subsystems). Combining just two subsystems of such quantum mechanical coins poses no problem, but in the field of quantum many-body physics, one deals with states in the state space of n such quantum mechanical coins. A general state in that state space is
Each subsystem, let’s say subsystem j, is again determined by its basis states, so ij can be either H or T. To have complete knowledge of the state, we need to know 2n numbers, which are stored in the tensor ci1,i2,…,in. For small n, this is not an issue, but the amount of information we need to store grows exponentially with the system size. Thus, storing this number of values on a computer can become a challenging task for n > 20. From this perspective, calculating or keeping track of the many-body wave function seems nearly impossible. Fortunately, people have realized that there are better strategies to encode (or compress) the information of the many-body wave function. These encoding or compression techniques are accomplished using tensor networks [2].
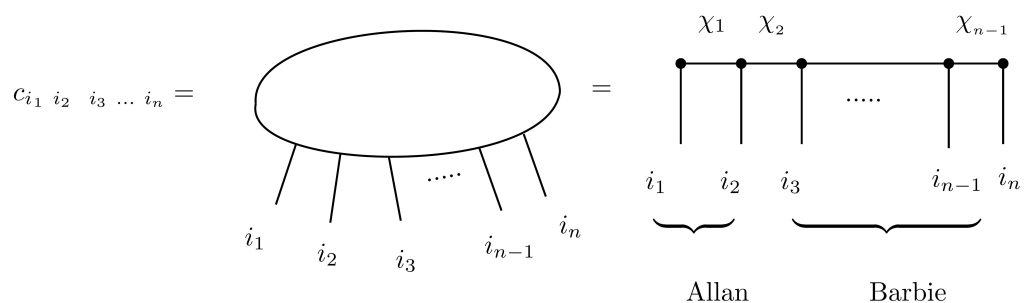
The idea is to rewrite the tensor ci1,i2,…,in as a contraction of smaller tensors, which can be done without any approximation. However, doing it exactly still means you have to keep track of an exponentially large amount of numbers. The main idea is that if I divide my system into two subsystems, Allan and Barbie (as shown in the picture), and the entanglement between them is small, I can significantly reduce the index χ2 to a smaller one, χ′2, without losing much information about the state. In practice, this approach has proven to be very successful, especially in one-dimensional systems, as it allows storing low-entanglement states with a polynomial amount of numbers instead of an exponential amount.
References
[1] Leonard Susskind and Art Friedman. Quantum Mechanics: The Theoretical Minimum, volume 2 of The Theoretical Minimum Series. Basic Books, New York, 2014.
[2] D. Perez-Garcia, F. Verstraete, M. M. Wolf, and J. I. Cirac. Matrix product state representations. Quantum Info. Comput., 7(5):401–430, jul 2007.